Oarblade Efficiency
© 2001 Atkinsopht (09/15/10)
Overall (and instantaneous) blade efficiency is defined as total oarhandle
effort (work) less blade (work) losses divided by total oarhandle work:
(Wkhndl -Wklosses) /Wkhndle. The oarhandle work less the blade losses is the
work done at the oarlock to propel the shell. Blade efficiency has little to
do with the direction or magnitude of the propulsive force. At mid stroke the
effort tends to be at a maximum but so too then is the blade slip loss. In
fact, slip loss is pretty much related to effort so, without detailed
analysis, it would be hard to say at what stroke point the blade efficiency
would be a maximum or a minimum. It is better to limit discussion of blade
efficiency to its overall value for the stroke.
I have recently (02/04) added to the ROWING model an instantaneous
calculation capability for the blade efficiency during the drive; the result
is shown in Figure 1:
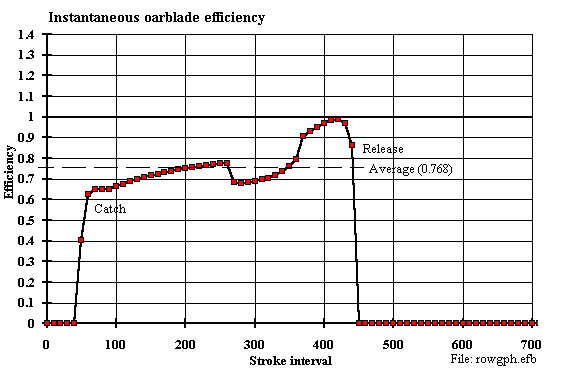
Figure 1. Oar Blade Efficiency
The result shown is for a single scull, heavy men, based on empirical data
from V. Kleshnev of the Australian Institute of Sport. As would be expected
the blade efficiency is "all over the place" depending upon the vagaries of
oarhandle force, instantaneous shell speed, and ephemeral values of blade
angle of attack and lift and drag. It is hard to see an obvious pattern which
might tell one that the efficiency is expected to be best at some particular
point in the sweep. It is, of course, a result for a totally immersed flat
plate; there being no better data available.
I invite comment on the seeming improvement at the end of the sweep, but
keeping in mind that at the sweep ends forces (and blade losses) are near
zero.
Recently I have come across some new work on blade efficiency by
Macrossan & Macrossan which tends to corroborate the
findings here. They analyse real data actually taken on the water and their
results in Figs. 9-13 show characteristics and magnitudes similar to those in
Fig. 1 above. The exceptions are that they show high efficiencies at the catch
and show no obvious "notch" in the middle--an artifact of the stall point of
the flat plate model.

