Cast a vote here if you think it should move up in the Top-100 ranking:

You will be transferred to the Top-100 site, but may then return here by going "BACK"

 Rowing Computer Research
Rowing Computer Research

This website and the research it represents is a work in progress.
The utility of a reasonably good computational model of any system is not that it can produce perfect absolute results but that it can produce good relative results. In no other way can changes in a variable of interest be evaluated while all others are held constant. With ROWING I would be unwilling to predict individual race results for any collection of boats and crews. But, because ROWING considers every significant variable, I have confidence in ROWING's ability to predict an advantage for a difference between one mode of rowing and another.
Atkinsopht will share information with any rower, coach, or crew wishing to understand the possible benefit of a rational approach to improvement in oar blade efficiency and shell speed. Get in touch with me.
A computer model treats only of the mechanical aspects of rowing and rowers. Crews win races through their capacity to add to the base mechanical skill of body and equipment those crucial elements which one can hope will never lend themselves to modeling: teamwork, resolve, spirit, etc. Beneath these intangibles, however, it behooves any winning crew to tune its mechanical base to the highest practical degree.
Note: I have done what I can--with a model written to compute in English units--to present results in metric units.
Note: See also a new third (2010) rowing computer modeling site by Roosendaal
A recent (2014) entry into the rowing modeling world is "FIRM" (Free Internet Rowing Model) by Leo Lazauskas of Australia.
1. Blade Surface Area-
The ROWING model indicates that
blade surface area should be as large
as a rower can easily manage. This is the first and easiest thing a rower or
crew should work on in order to increase efficiency and speed. And, perhaps too,
he should look into the "Greenland" blade.
Also NEW (03/02/16) in Blade Surface Area: See here the Concept2 new small
Bantam blade by comparison with the larger Fat2.
2. Peak Force Management-
The ROWING model indicates an optimum point and timing for the
peak of the oarhandle force profile
in the course of the drive. Intuition might tell one that the peak force
should coincide with the oarshaft ninety-degree point- a correct hunch as it
turns out. This technique will be hard to learn without direct oarhandle
force feedback available on the boat itself- the next wave for N-K?
3. Rower Strength & Rigging Geometry-
The ROWING model shows that there is, for every rower, a best
oar length and lever ratio depending
upon the rower's peak oarhandle pull (his strength) thus providing a rational
approach to the optimization of rigging arrangements. An example is given for
coxless fours. This, too, will be hard to implement without the same force
feedback instrumentation suggested above.
4. Managing the Free Return-
The ROWING model indicates that there is no possible way to
coach the free return
for improvement in shell speed, except by increasing the "float".
5. Peak Force vs. Rating-
The ROWING model shows that it seems better to
pull hard at a lower rating than to ease up
at a higher rating; all while doing equal rower total work.
6. Catch Bow Angle-
The ROWING model indicates the
optimum catch bow angle and allays
fear of the worrisome "pinch-point" for scullers.
7. Blade Cant Angle-
The ROWING model indicates an
optimum cant angle between oarshaft &
blade which may avoid current physical restrictions on smaller catch bow
angles for sweeps.
8. Peak Oarhandle Pull-
The ROWING model indicates that a ten percent increase in rower peak
oarhandle pull can be expected to yield a 3-1/2 percent increase in
average shell speed at equal stroke rating. For an eight this translates
into about three lengths in 2000m. Total rower power would increase about
7-3/4 percent; just about what would be expected from theory: P2/P1 =
(V2/V1)3. Of course, for equal rower power, pull force can be
traded off against rating; it seeming better to pull hard at low rating.
9. Oarshaft Flexibility-
The ROWING model indicates that oarshaft flexibility has virtually
no affect on shell speed. Flexibility modifies oar handle (torso) speed
and momentum but in such a way as to produce no change in the net work
transferred to the oarlock or footboard. Flexing a well made shaft is
efficient (little lost heat generated); however, opting for stiffness can
conserve a bit of energy, but may be hard on the
rower's back.
10. Blade Immersion Depth/Puddles-
It seems reasonable to expect that a
well buried blade will be more
efficient than one limited to the water's surface.
11. Oarblade Efficiency-
Instantaneous or position dependent
oarblade efficiency is not a very
useful concept.
12. Shell Speed vs. Lever Ratio-
Shell speed varies with oar lever ratio. There may be
a best value for this variable.
13. Shell Speed & Course Time vs. Air Drag-
Shell speed varies with
air resistance.
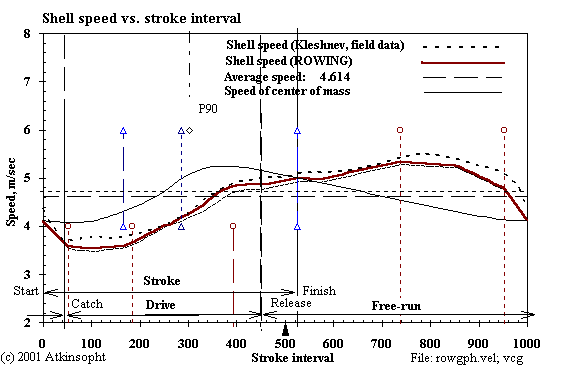
The speed profile is a function of the movements of the rower's mass on the slide and the speed and forces at the oarhandle.
1. Oarblade Path Geometry- The absolute slip of the oarblade is large in spite of convincing appearances to the contrary.
2. Propulsive Force- The propulsive force exerted "on the water" by the oarblade has little to do with blade design or hydrodynamics.
3. Oarblade Vectors- In the literature I have found no consistent exposition of the forces and velocities pertaining to an oarblade in the water slipping under load. This new presentation is a simplified one; for more detail see Oarblade Lift and Drag.
4. Oarblade and Wing Compared- The oar blade is not exactly an airplane wing.
5. Oarblade Lift and Drag- How lift and drag affect oarblade slip.
6. Shell Work- A significant portion of the useful effort required to advance a shell is transferred through the footboard.
7. Rower Power- Total rower power output includes the internal mechanical work done on the rower's own body, and which is there lost internally in friction and heat. To date this internal work has been almost universally ignored in rowing research.
8. Drive/Return Ratio- There is confusion in understanding the relation between stroke rate and drive/recovery (return) period ratio.
9. The Moving Water Fallacy- Oarblades do not "move" masses of water around while sweeping the stroke.
10. Shell Hull Friction- Data are sought for shell hull block and prismatic coefficients.
11. Soccer Balls for Oar Blades?- Soccer balls work well enough as oar blades but are not recommended.
12. Water Temperature- Shells go faster in warm water.
13. Asynchronous Rowing- Can the elimination of cyclical speed variations increase shell speed? The answer is no.
14. Coxswain on Sliding Seat- Perhaps tomorrow's cox can be enjoined to help out.
15. Counting Strokes- Racers would do well to pay attention to course stroke count.
16. Some Observations- Further research, propulsive efficiency, on-the-water testing, design, etc.
17. The Effect of Deadweight The effect of dead (displacement) weight on shell speed.
18. Shell Hydrodynamics- How ROWING makes shell resistance estimates.
19. Rigging Notes- How span and spread changes affect oarshaft angles: not by very much. And how span and spread changes affect "gearing": virtually not at all.
20. Upstream/Downstream- How rowing river currents upstream or down affects the power required for rowing.
21. Shell Air Resistance- It's time for someone to measure shell air resistance; here's how.
22. A Useful Empirical Equation- Quickly make estimates for new shell speed for changes in stroke rate, pull force, and fluid resistance.
23. Race Start- Fifty percent of race speed is achieved by the end of the first stroke.
24. Big Blades and Back Injury- Oar shaft flexibility may be able to compensate for increased blade surface area.
25. Sliding Riggers- Sliding riggers are fast but banned in competition.