Cast a vote here if you think it should move up in the Top-100 ranking:
You will be transferred to the Top-100 site, but may then return here by going "BACK"
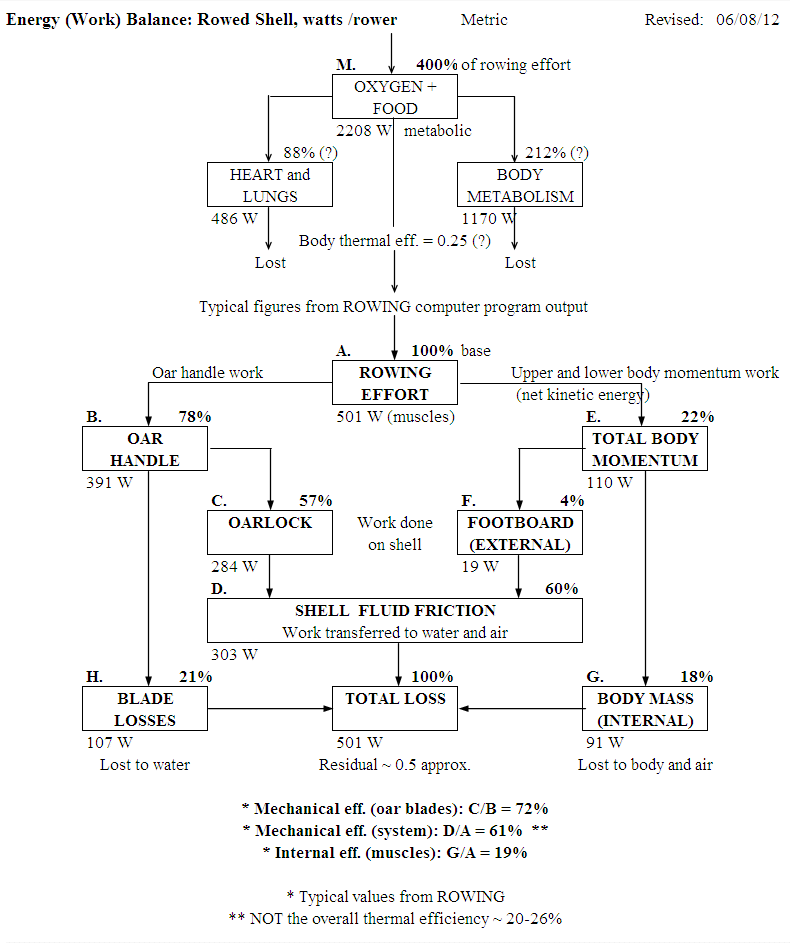Figure 1
At the top of the figure I have noted an estimate of the total metabolic work that would have been measured by an oxygen consumption calorimeter.
The figure reveals the generally unforseen useful work (the kinetic energy of momentum transfer) delivered to the shell via the footboard - a significant part of the rower's total effort (also identified by V. Kleshnev of the Australian Institute of Sport). Researchers in the field of rower power and biomechanics must learn to measure and to take this work into account. Not everything useful is accomplished overtly at the oarlock.
The net work applied to the shell (the residual) must sum to near zero over the stroke as the shell average speed is constant, that is, there is no net acceleration. The works at B, H, F, G, and D are calculated independently of one another- none are found by difference. The required zero sum is the result of the algebraic combinination of the works at C, F, and D. Calculation iterations proceed until the residual, (C+F)-D, is acceptably small.
The momentum work appears in two modes - an "external" mode in which work is done directly on the boat and a complementary "internal" mode in which the work (of the same forces) is done on the rower's body and dissipated there as a loss through internal friction and heat.
The external momentum work can be as high as ten percent of the total work output and appears at the footboard - the rowers' only point of contact with the boat other than the oar handle. In my experience only one other researcher has recognized this work as part of the effort contributing directly to the advance of the shell. Thus, when making biomechanical measurements of the rowers' effort in rowing, it is a mistake to consider only the work done at the oar handle. And of course, on an ergometer, it is not even possible to measure external momentum work because there is none (the footboard is fixed). This difference raises fairness issues when comparing stationary "rowers" of differing heights and weights.
The internal work can be twice the external work and is an irrecoverable loss. The signs of the internal works (positive in the direction of the shell motion) in the various portions of the stroke cause the algebraic sum of the internal works to equal zero; a necessary condition since no net work (acceleration) is done on the rower's body. The negative work done in re- accelerating the slide after the finish - in the free return - exactly equals the positive work done in re-decelerating the slide to the start no matter how the accelerations are managed. Note, though, that it is the absolute values of the internal works that sum to the internal work lost because the body has virtually no energy storage capacity (no springs or accumulators). I will look into ways by which the management of momentum may reduce the internal work losses.
Because I charge the internal work to the total rower power I obtain higher overall powers than do most researchers - who neglect it because it is difficult to measure directly. In the example illustrated the rower total power is about 552 W. The system mechanical efficiency is about sixty percent and the oarblade efficiency about seventy-five percent. The rower's thermal (metaboliic) efficiency (measured by oxygen uptake), however, will always be in the vicinity of twenty-five percent.
Of the total work done at the oar handle about three quarters appears at the oarlock; the rest being dissipated in losses to the water in slippage and turbulence at the blade.
The value of results from a model is that all variables may be included and that, for comparisons, any set of variables unrelated to the study at hand may be held constant. Total rower output is a good example - easy to estimate accurately in a model and difficult to measure in the real world.
It is reassuring to any investigator to find his work in agreement with the work of another. Such is the case here in comparing rowing efficiencies with those estimated by Kleshnev . We have power and efficiency figures as follows:
Ptot- Atkinson 552w (A, Figure 1); Kleshnev 544w
Pmet= Atkinson 2208w (M, Figure 1); Kleshnev 2386w
Rower "Delta" (metabolic)- Atkinson 25% (A/M); Kleshnev 23%
Oarblade- Atkinson 75% (C/B); Kleshnev 79%
Kleshnev does not address the system mechanical efficiency, 61% (D/A), which is analagous to that of the output of a driving engine, 552w; in relation to the "useful" work done by its driven machine, 336w.
Note: In answer to a query from a reader I offer the following clarification of the descriptions of the work done on the shell at the footboard:
The footboard work is the sum over the stroke of the incremental force at the footboard times the incremental shell distance traveled in the incremental time interval (1/1,000 intervals /stroke); dW=Fds. Part of this force is the pure (equal but opposite) reaction to the rower's pull on the oarhandle and a smaller amount the result of the forces generated by momentum exchange with the lower (hips portion) and the upper (torso portion) of the rower's body. I call it footboard work although it could just as easily be reckoned at the gate.
The incremental momentum works on the rower's body sum to zero (cancel out as they must)* over the stroke but the same incremental momentum works on the footboard (shell) do not because- while the incremental momentum forces between the two (body and shell) are always the same- the distances traveled in the same time interval are not. This difference amounts to net work done on the footboard and augments the speed of the center-of-mass of the system through friction (propulsive) contact with the water.
* The calculated (mathematical) positive and negative internal works on the body sum to zero but the actual internal work done is the sum of the absolute values because the drive and return work is done by different muscles and because muscles do not store energy as if they were springs.
I have not really tried it myself but I believe that a boater, through the agency of this fluid friction, could marginally move a boat in the way that a child can move a wagon by the same means (whereas an astronaut in absolutely frictionless space cannot).
This leaves remaining the question as to whether changing the mode (but not the frequency) of a given momentum exchange can affect system speed. It appears, from the results of the computer model, that it cannot. The result of running cases with the ROWING model with greatly varying momentum modes (all other variables being equal) shows always the same net work at the footboard in all cases and no effect on the speed of the center-of-mass of the system.
Some interesting and confirming work by van Holst is germaine to this discussion. He too, with me and Kleshnev, finds a net positive shell propulsion contribution by the rower's external momentum work (F, Figure 1) and concludes, in addition, that varying momentum modes on the slide can have no effect on the speed of the center-of-mass of the system.