Figure 1
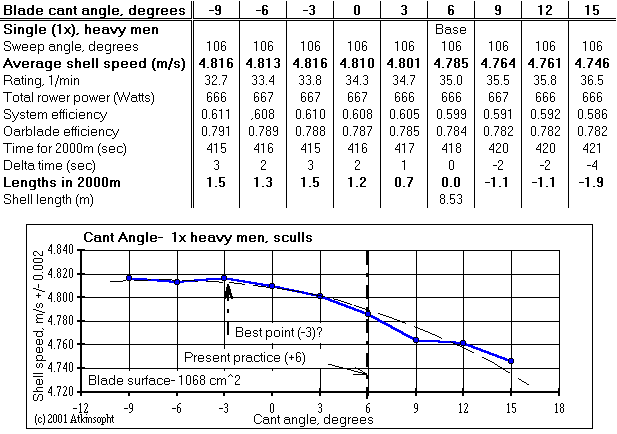
The results show that scullers might profit by eliminating cant from their blades. The removal of cant seems analogous to tightening the catch bow angle. See the discussion on catch bow angle, Figure 1.
Figure 1
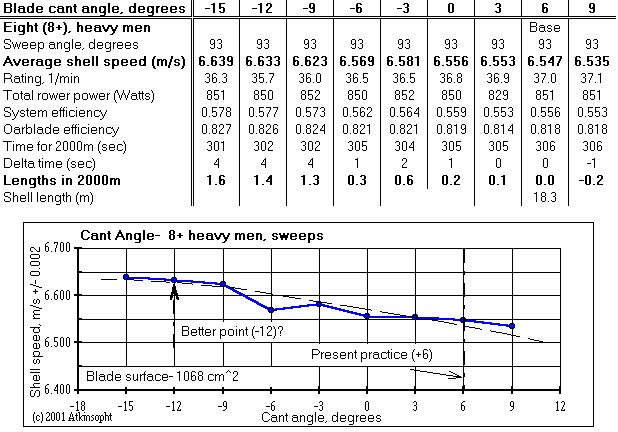Figure 2
"Sweepers" might profit by experimenting with negative cant. Cant
reduction seems analogous to tightening the catch bow angle--seen as desirable
for sweeps but difficult of attainment through rigging changes. See the
discussion on
catch bow angle, Figure 2.
Up to a point (probably approaching that of the catch bow angle) negative
cant increases the zero-slip shell advance per stroke- that is, it reaches
for a longer "bite" of water at the catch. Negative cant long ago appeared in
the paddles of serious downriver canoe racers.
Large degrees of cant must be realized through careful design. In order to preserve ease of feathering the axis of the oarshaft should pass through the center-of-mass (and pressure) of the blade thus producing a trailing edge--at the catch-- free of the shaft as shown in Figure 3. Even so, feathering will be harder owing to an increased blade mass moment about the oarshaft axis. Adjustments for pitch will be less direct and may have to be incorporated into the blade design itself. Note that the cant angle should never be such as to urge or to drive the blade toward the boat at the catch.
Note that a degree of negative cant equal in magnitude to the catch bow angle (about 20 degrees for sculls- more for sweeps) would render it (theoretically) impossible, through bad management of the catch timing, to generate backsplash ("sidesplash" yes; backsplash no). This is because in this circumstance the blade at the catch is aligned exactly with the shell's direction of motion.
"Catchsplash" of any sort is wasteful of energy and backsplash has the added disadvantage of imparting a small- but real- momentary check to the advance of the shell.
ROWING does not model the inefficiencies of catchsplash or of insufficient blade immersion but their general effects can be inferred from first principles.
Figure 3 shows typical zero-slip and actual sweep blade loci for a negative cant angle of ten degrees.
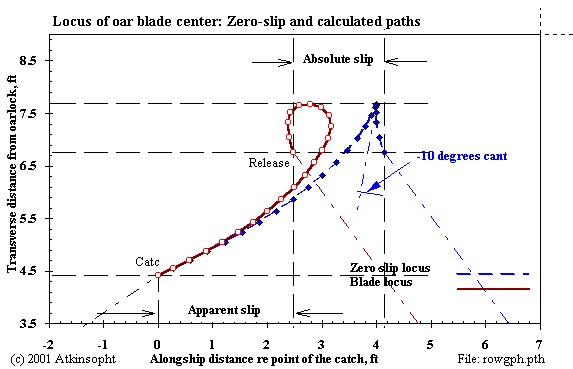Figure 3
Figure 4 shows the corresponding lift and drag profiles.
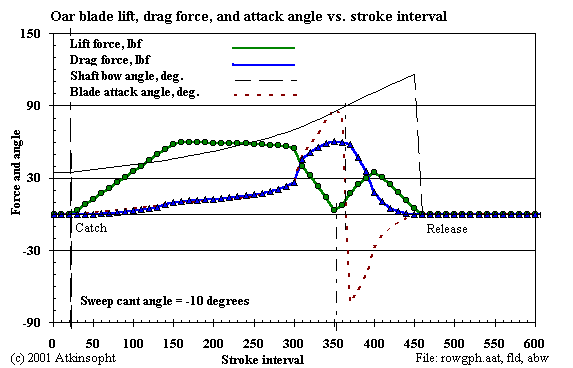Figure 4
The simplest explanation for the advantage of a backward canted blade is probably its lengthening of the zero-slip blade path. The longer this path the greater the no-slip advance of the shell per sweep. For a given blade slip (an inefficiency) the shell advance improves with negative cant.
Perhaps, too, the advantage of a backward canted sweep blade, as shown in Figure 5, is owing to the extended period of lift it offers to the onset of the stroke although how this works is hard to visualize.
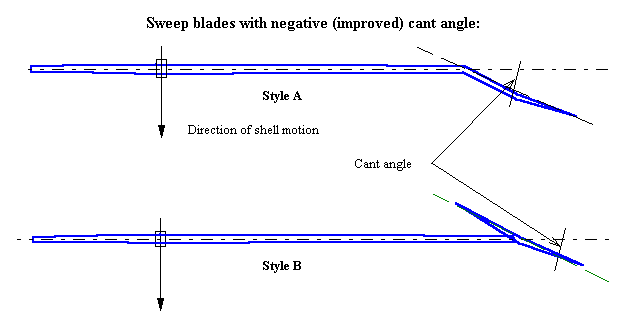Figure 5
The result is that at equal rower total power performance suffers. The difference lies in the fact that, for the same catch and release bow angles, the modified blade has a much smaller theoretical and actual shell advance per stroke. As much as half as much- requiring the rower to double the number of strokes required to cover a specified distance.