Catch Bow Angle

© 2001 Atkinsopht (08/29/16)
The bow angle of the oarshaft at the catch is a subject of debate-- especially among scullers--who have argued long over the so-called "pinch- point" and its effect on the way of the boat. The discussion centers on whether a shallow angle wastes power by unnecessarily thrusting water sidewise at the catch.

Bow angle: The angle between the oarshaft and the longitudinal axis of the shell; zero at the bow, 90 degrees athwartship, and 180 degrees at the stern; "theta" in the diagrams and expressions in this paper.

Sculls


Figure 1 shows the result of calculating average speed for a single scull with varying degrees of catch bow angle but with equal overall sweep arcs, equal oarhandle force profiles, and at equal total rower power output. Twenty-five degrees at 35 1/min is the base case as this seems near the value common in race practice. Because total rower power is held constant the rating varies somewhat from case to case.

Figure 1 Figure 1

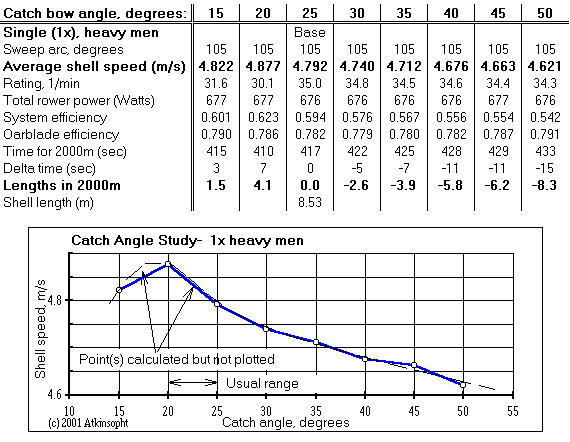
The result seems to show that scullers--either through evolution or good fortune--have hit upon the near optimum catch bow angle and that to err on the small side has no concealed "pinch" penalty. Scullers might want to experiment with reducing the current blade cant angle from about six to zero degrees. Easiest might be to reconsider the Macon blade if that can be done without sacrificing blade surface area.

I have recently (2016) had a communication from Havaard Grunnvaag of Norway pointing out that ROWING's computer optimised bow angle (20 degrees) is essentially the same as Kleshnev's conclusion (68-70 degrees) arrived at by empirical means. (Note a 90 degree phase difference in our angle reckoning.) I'd like to think that this agreement says something about the validity of our corresponding work.

Sweeps


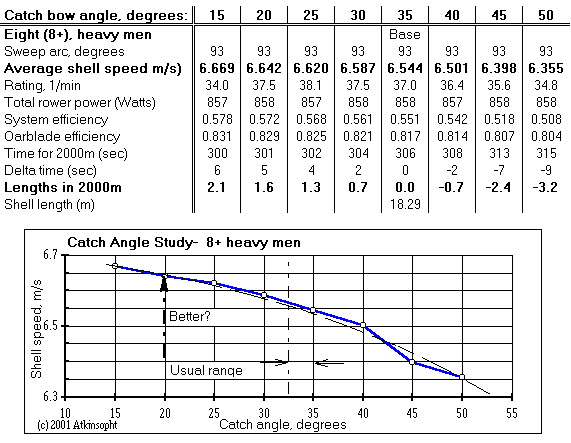Figure 2 shows the result of calculating average speed for a coxed eight with varying degrees of catch bow angle but with equal overall sweep arcs, equal oarhandle force profiles, and at equal total rower power output. Thirty- five degrees at 37 1/min is the base case as this seems near the value common in race practice. Because total rower power is held constant the rating must vary from case to case.

Figure 2 Figure 2

The result seems to show that "sweepers"--for geometrical reasons--have been unable to avail themselves of an optimum catch bow angle. At small angles the sweep oarhandle is awkwardly out of reach over the saxboard at normal rigger spreads. And if the spread is reduced to better this condition the mid-stroke handle arc swings just as awkwardly out over the opposite side.

Innovative coaches and boat, and oar designers may be able to improve catch conditions somewhat for sweep boats but it doesn't look easy. Tinkering with as much reduced spread as remains practical may have some small benefit-- but see the ROWING blade cant angle results. Sweepers should consider testing blades with negative cant. If I were an oarblade designer negative cant for sweeps (and zero for sculls) is absolutely the first thing on which I would experiment.

Home Page Site Map Rowing Page