Cast a vote here if you think it should move up in the Top-100 ranking:

You will be transferred to the Top-100 site, but may then return here by going "BACK"

The zero-slip locus of the blade center is the path followed under zero load at the handle, that is, the path followed by a flat-bladed oar dropped, in a moving boat, into the water at the catch angle and simply allowed freely to float or drift through to the release angle. Few eddies form and the blade leaves the water well ahead of the catch point. (See Figure 1) The zero-slip path is theoretical, a tractrix, and no real blade of any kind would exactly follow it - but it is ideal as a standard reference for comparisons between the slips of various blade forms.
Another way to visualize the zero-slip locus is to consider an ice boat whose oarblades are figure skate blades constrained by their bite in the ice to move only along their chords.
A non-zero lift coefficient at the zero degree attack angle affects the zero-slip path. Such lift acts like a change in cant angle by an amount equal to the zero-lift angle of attack and ROWING can take this into account. The free and unloaded blade always seeks the path of zero lift.
Without knowledge of the zero-slip path the absolute slip of an oarblade cannot be determined. Thus, it is necessary that any rowing model calculate the zero-slip locus. Conveniently, this path is closely approximated by a well known mathematical curve called the tractrix. If the blade has no (cant) angle to the shaft - and zero lift at zero attack angle - the curve can be treated as a simple "right" tractrix. However, most blades have an average cant angle of about six degrees - and perhaps significant lift at zero angle - and the tractrix then becomes "oblique"; a more complex mathematical problem.
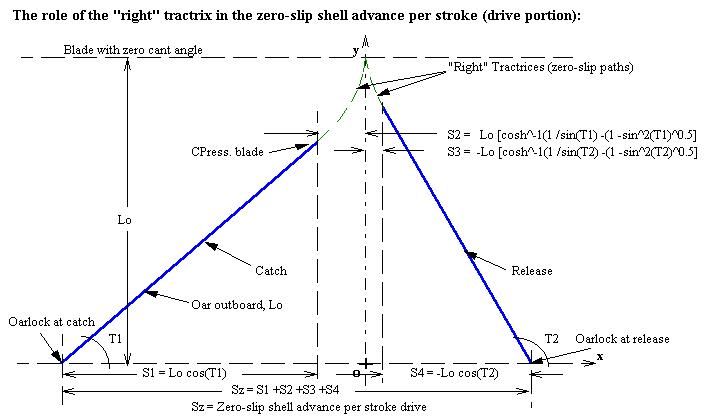
The zero-slip advance of the shell (the oarlock) per stroke (Sz) is the sum of four distances, for a blade with zero cant angle, as illustrated above. When the cant angle is not zero the tractrix becomes "oblique" or skewed and the calculation of values for S2 and S3 becomes more complex than is shown in Figure 1.
A Slip Calculator:
In principal a device could be designed to determine the absolute slip of
an oarblade on a boat in real time. By using the known (fixed) geometry of
the oar and by sensing the catch and finish angles (and their instants in
time) the mathematics can directly calculate Sz = S1 +S2 +S3 +S4, the zero-
slip (theoretical) shell advance per drive relative to the water. Then, by
using the output of the N-K (or other) speed sensing device the actual shell
advance for the same drive interval can be found. The difference in the two
drive advances is the absolute slip and could be continuously displayed on a
monitor.
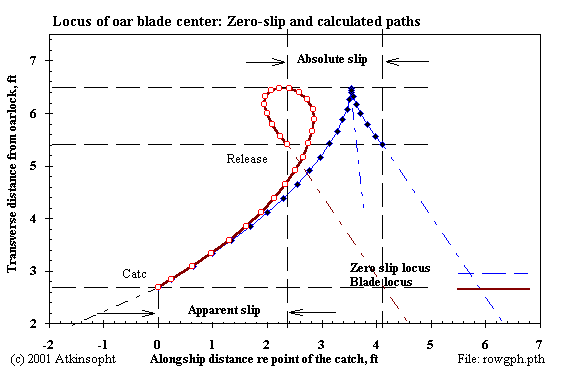
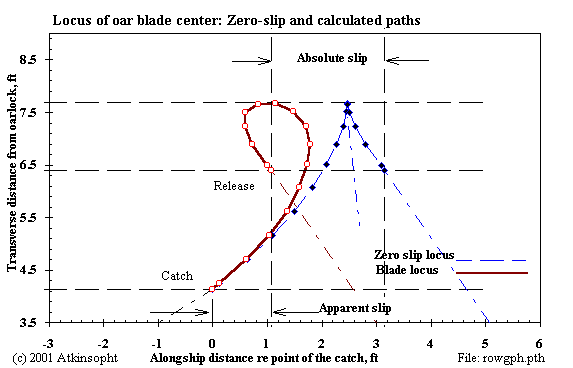
Under the rower's effort at the handle the blade slips continuously, increasingly departing from the zero-slip ideal path as the stroke progresses. Shaft transverse slip increases as force increases and decreases with increasing blade surface area and drag coefficient. When the force is near zero- at the stroke ends- the ideal and actual blade paths are parallel. And, when the force is at a maximum the two paths are at right angles to one another (Figs. 2 & 3). Total slip is less as the time spent by the blade in the water is less; that is, as the stroke rating goes up. The hydrodynamic force of lift has a smaller effect than might be expected (see the section on lift and drag). Slip reduces the blade efficiency and the advance of the shell per sweep but has virtually no effect on the rower's propulsive force on the shell.
ROWING defines sweep effectiveness as the ratio of actual shell advance per sweep to theoretical (zero-slip) advance per sweep. Shell advance per sweep is not the same as (is less than) shell advance per stroke. Sweep effectiveness is closely related to oarblade mechanical efficiency.
Ken Young of the University of Washington made good photographs from a bridge (as have others) which show the actual blade locus, but he did not photograph the zero-slip path so from it he could learn nothing about the slip. This is easily done by photographing the blade sweeping the zero-slip locus (under zero handle load) as described above. I urge someone who reads this to go out to some handy bridge and actually do it for the record.