Atkinsopht/Rowing/Managing the Free Return Momentum

-o0| At the end of having browsed in this site |0o-
Cast a vote here if you think it should move up in the Top-100 ranking:
You will be transferred to the Top-100 site, but may then return here by going "BACK"

Managing the Free Return Momentum

Coaching Note-

Slide on the free return-
At constant rating there is nothing the rower can do in the free return directly to alter the speed of the system center-of-mass. Nothing can be gained purely by changing the relative effort put into the taking off from vs. the landing onto slide stops (See Figs. 3 & 4 below).

However, there is a definite conservation of rower effort to the extent that "float" can be encouraged or achieved between leaving and hitting the stops. During the float interval no work is done by the rower. This gain cannot show up as a direct change in the speed of the system center-of-mass, but it does mean that the energy saved can be expended elsewhere, i.e., at the oarhandle or in a rating increase which can then increase the speed of the shell.

Slide on the drive-
The same can be said of slide motion in the drive. It makes no difference dynamically whether a rower "shoots" the slide or not- or commits some other drive momentum sin- as long as his slide motion does not compromise the strength, timing, and efficiency of his pull on the oarhandle. A small float saving might be realized here as well but it is hard to imagine how it might be achieved or recognized.

Managing the effort at the oar handle is probably more important than managing the motion of the slide.

Rowing "Style"-
It is my conclusion that- except insofar as a rowing "style" may enhance or compromise the strength, timing, and efficiency of the pull on the oarhandle- style (as reflected in the shape of the shell speed curve at constant rating) has no effect on the average speed of the system center-of-mass.

Some confirming work by van Holst is germaine to this discussion. He, too, concludes that varying momentum modes on the slide has no effect on the speed of the center-of-mass of the system.

I do not mean to imply that rowers (in other than singles) should not "swing" in perfect synchrony and harmony with their mates; it is just that one brand of synchrony is probably almost as good as any other.

Races are won not on a particular style but on strength, proper peak-force management and rigging, endurance, race pace strategy, and esprit de corps.

Free Return "Modes"-

The ROWING model shows that, for a given "mode" at constant rating, it is not possible to alter the average speed of the shell or of the center- of-mass by changing the way in which the rower's body mass accelerations are managed in the free return- from the finish to the start of the stroke. Furthermore, except in the presence of float (see above), the net useful work done at the footboard remains independent of the acceleration management.

The ROWING model shows that, at constant total rower power, it IS possible- but only indirectly- to alter the average speed of the shell by changing the "mode" by which the rower's body accelerations are managed in the free return. One "mode" can be seen to require more or less rower return energy than another thus making the difference available for work and endurance in the stroke.

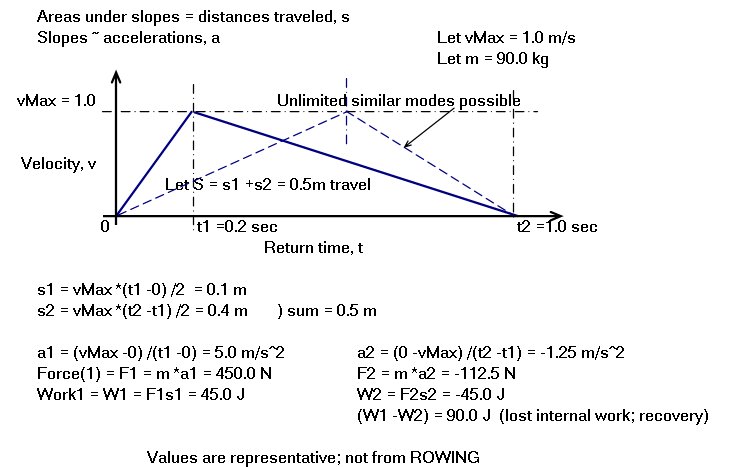
Two modes of momentum management are considered; one which I will call triangular and one I will call trapezoidal. For clarity the modes investigated employ only uniform accelerations (constant forces) and treat the torso and the slide as having their various speeds and travels in unison- not really the case on the water where the torso generally precedes the slide in the return.

Triangular Mode-

In the triangular velocity distribution mode the rower uniformly and simultaneously accelerates his torso and slide masses to some point of the return distance and then, instantly, begins a uniform deceleration to full compression at frontstops. This produces a triangular profile when shell- relative speed is plotted against time. The profile resembles a peaked roof and the area of the "gable end" thus formed represents the total (fixed) distance travelled. If the rower pulls hard off backstops and eases smoothly onto frontstops the gable is asymmetric- steep at first and then more gently sloping. The rower may produce equal acceleration and deceleration in which case the gable is an isosceles triangle. He may ease off backstops and hit hard onto frontstops producing a gable shallow at first; steep at the end. In all three cases the height (velocity) of the peak is constant at constant rating and the enclosed areas are all equal (the same distance travelled).

Uniform accelerations produce constant forces and so the areas under corresponding force plots represent the internal work done by the rower on his own body. The positive work done during the acceleration is always exactly equal to the negative work done during deceleration.

So- for triangular velocity distribution- whether the rower starts hard off the finish and eases onto frontstops or eases off the finish and comes hard onto frontstops makes no difference whatever to the average speed of the boat. The works done during the slide acceleration and the slide deceleration in each case are virtually identical even though the forces are very different. The small force over a long time equals the large force over a short time.

This result can be further understood by considering the shell speed curves for the center of mass. During the free return the system is under the influence only of hull and air fluid friction; its speed will decline asymptotically toward zero (reaching zero in infinite time). As long as the oarblades are out of the water no action of the rowers can significantly change the average speed of the mass center (which always equals the average speed of the boat). The motions of the hull itself will differ in each case but the overall speed remains unaffected.

The same conclusion has been reached by Marinus van Holst who has independently modeled the triangular mode on the slide "3. Variation of seat speed during recover[y].".

Figure 1

Trapezoidal Mode-

In the trapezoidal velocity distribution mode the rower uniformly and simultaneously accelerates his torso and slide masses to some point of the return distance and then begins a period of constant velocity (zero acceleration) before making his uniform deceleration to full compression at frontstops. This produces a trapezoidal profile when shell-relative speed is plotted against time. The profile resembles a flat roof with gable ends and, again, the area of the profile thus formed represents the total (fixed) distance travelled. If the rower pulls hard off backstops and eases smoothly onto frontstops etc. the gables are asymmetric as described above.

Again, uniform accelerations produce constant forces and so the areas under corresponding force plots represent the internal work done by the rower on his own body. And again, the positive work done during the acceleration is always equal to the "negative" work done during deceleration.

So- for trapezoidal velocity distribution (and equal constant velocity periods)- whether the rower starts hard off the finish and eases onto frontstops or eases off the finish and comes hard onto frontstops makes no difference to the average speed of the boat. The works done during the slide acceleration and the slide deceleration in each case are virtually identical even though the force distributions are very different. The small force over a long time is equivalent to the large force over a short time.

The extent to which a rower can take advantage of this knowledge is limited by his strength and the strength of his tissues; the ultimate advantage requiring forces well beyond human capability. As far as I know measurements of such body limits have not been published.

Figure 2

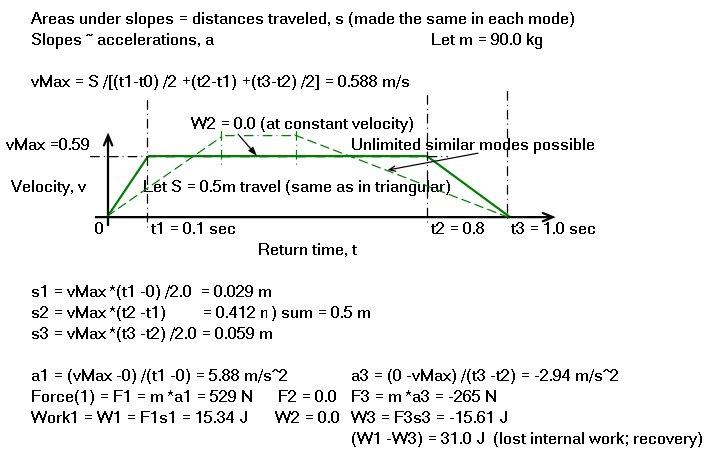
Note that, for a given time, t, spent in the free return, the area under various velocity curves must all be equal because they define the distance traveled- by the body masses- which remains constant.

At Equal Total Rower Power-

However, under conditions of equal total rower power the trapezoidal mode is faster than the triangular mode.

ROWING shows that it is better to accomplish both the acceleration and deceleration quickly leaving as much time as possible in the middle for a constant velocity, zero-force, "float" to frontstops. The steeper the accelerations on either end of the float the higher the rating and the faster the boat (for equal total rower power expended).

The reason is that in the triangular mode the rower's per-stroke internal work requirement is higher than in the trapezoidal mode. He is doing work during the entire length of the return path whereas, in the trapezoidal mode, zero work is required during the "floating" portion. Relieving the rower of this internal work load (all of it a loss) permits him to direct the work saved to an increase in rating and, consequently, of shell speed. It is the increase in rating for the same power output that permits the gain. The shape of the return portion of the shell speed curve flattens. The shape of the center-of-mass curve and the "check" (the speed curve amplitude) remain essentially unaffected. Thus, the gain is not the result of a lessening of the shell speed excursion above and below the average speed.

Whether coaching to optimize return momentum management is a successful strategy is not clear; it is certainly a subtle matter. The time period is short, the forces large, and the result essentially hidden from view- until the makers of rowing electronics can provide instant body mass and shell speed curve "readouts" for analysis.

Momentum Work Frames of Reference-

The fixed frame of reference, for what I term the "internal" momentum work, is the shell; and the frame of reference for the "external" momentum work is the water (the world). These two works sum to the total momentum, indirect, work done by the rower on the system. Momentum work is done both in the drive and in the free return. The remaining portion, the direct work, is done on the system at the oarhandle. See the section on shell work.

The rower's instantaneous horizontal footboard force and his incremental distance travelled on the slide relative to the shell determine the incremental internal work done (on his own body).

And the (same) horizontal force and the shell's incremental distance travelled relative to the water determine the rower's external work done (on the boat).

The momentum works of the upper body (torso) and of the lower body (slide) are calculated separately before combination. It is a requirement of the system that the (algebraic) sum of all internal momentum works be zero (see below).

In the free return the ROWING model finds the total time available and then calculates the instantaneous footboard force from the defined "mode" and its resulting instantaneous accelerations.

Some Numbers from the ROWING Model-

1. Triangular mode

Free return for a typical coxless four:
Acceleration           Float  Deceleration
============           =====  ============
Mode A.
Time 0.83 sec (gentle)  0.00  Time 0.21 sec (steep)                       Avg.
Torso:      Slide:            Torso:      Slide:      Rating Rower Syst. shell
Force Work* Force Work        Force Work  Force Work         Power Eff.  speed
    N    J      N    J            N    J      N    J   1/min     W         m/s
----- ----  ----- ----        ----- ----  ----- ----  ------ ----- ----- -----
  160 -549    120 -240         -641  541   -489  236    34.0   705 0.453  5.30

*per rower

Figure 3

Mode B.
Time 0.21 sec (steep)   0.00  Time 0.83 sec (gentle)                      Avg.
Torso:      Slide:            Torso:      Slide:      Rating Rower Syst. shell
Force Work  Force Work        Force Work  Force Work         Power  Eff. speed
    N    J      N    J            N    J      N    J   1/min     W         m/s
----- ----  ----- ----        ----- ----  ----- ----  ------ ----- ----- -----
  641 -560    489 -240         -160  551   -120  237    34.0   708 0.454  5.31

Figure 4

Notice, above, that rower power and average shell speed are essentially unchanged by the swapping of accelerations and that the absolute free return slide-work is the same in each case (within 1%). When the slide-works are equal there is no change in the average speed of the shell or of the center- of-mass.

It must be understood that the work done on the rower's body is not algebraically zero as might be thought (although as far as the system is concerned it must sum to zero). Take the torso work in Mode B: accelerating(- 560 J) +decelerating(551 J). Although the sum is zero the work is done in each case by completely different muscle groups; thus there is no "negative" work compensation. As far as the body is concerned it is all positive work and is all lost in internal friction and heat (560 +561 =1,121 joules).

2. Trapezoidal mode

Free return:
Acceleration           Float  Deceleration
============           =====  ============
Mode A.
Time 0.31 sec (gentle)  0.44  Time 0.13 sec (steep)                       Avg.
Torso:      Slide:            Torso:      Slide:      Rating Rower Syst. shell
Force Work  Force Work        Force Work  Force Work         Power Eff.  speed
    N    J      N    J            N    J      N    J   1/min     W         m/s
----- ----  ----- ----        ----- ----  ----- ----  ------ ----- ----- -----
  360 -359    276 -159         -845  356   -649  156    37.8   702 0.506  5.49


Mode B.
Time 0.13 sec (steep)   0.44  Time 0.31 sec (gentle)                      Avg.
Torso:      Slide:            Torso:      Slide:      Rating Rower Syst. shell
Force Work  Force Work        Force Work  Force Work         Power  Eff. speed
    N    J      N    J            N    J      N    J   1/min     W         m/s
----- ----  ----- ----        ----- ----  ----- ----  ------ ----- ----- -----
  832 -363    636 -159         -356  358   -271  154    37.6   702 0.509  5.50

Figure 4-1

Notice that these two very different cases (triangular and trapezoidal) were run at essentially the same total rower power (within 0.64%), but that a speed gain of about 3.8% was realized in the trapezoidal mode. How is this possible? How is the average shell speed changed- along with that of the center-of-mass- by changing the mode of momentum exchange when we have argued above that this- by itself- is impossible?

It is owing to a reduction in the free return slide-work which, in modeling for equal total rower power- permits a corresponding increase in speed to consume that newly available power. Another way of looking at it is that the effort the rower saves on the slide now becomes available to him slightly to increase his pull or to increase his rating (note the increase in rating for the trapezoidal case). Here the interval between the two accelerations is executed at constant slide speed and, because the acceleration here is zero, requires zero force and zero work. I will call this zero-work phase "float" on the slide and will argue that it should be encouraged.

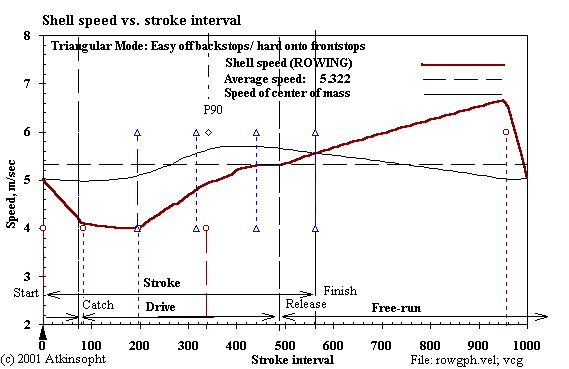
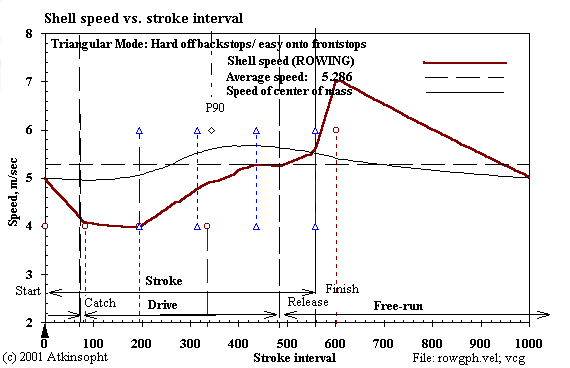
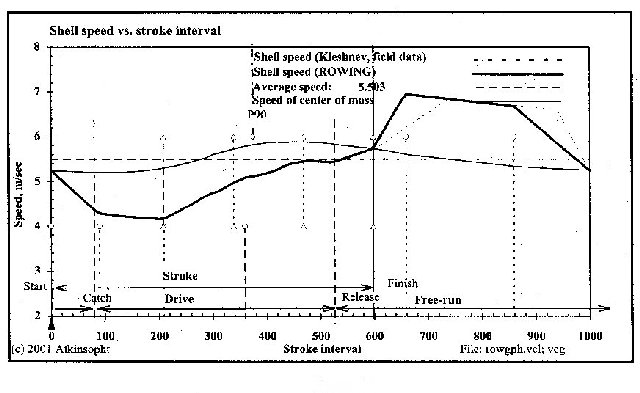
Notice that the free return "arc" in this case is not much different from the shape of speed curves taken from real shells on the water. So it may be that nature encourages rowers to take the least energy path without their realizing it.

The slide-work saved is the difference between triangular 1,566 J (549 +240 +541 +236) and trapezoidal 1,030 J (359 +159 +356 +156) or 536 J. The change to the trapezoidal mode has thus permitted an increase in the average shell speed from 5.3 to 5.5 m/sec; an increase of about four percent.

-o0|0o-

More on the Concept of "Float"- (10/24/10)

Subsequent to a recent exchange of views between me and an experienced rower and coach I have looked further into what might be gained by coaching "float" on the slide during the free return. For the ROWING model three modes have here been defined for a typical single scull with a 90kg rower.
1. A base mode in which the management of the return momentum on the slide is more or less "triangular"- in particular- forty percent of the slide excursion assigned to mass acceleration and forty to the corresponding deceleration (40-20-40). The return portion of this shell speed curve looks much like most such "real world" profiles.

2. A "trapezoidal" mode in which a period of 50% float has been introduced in the center (25-50-25); all other input variables being held constant. This return speed profile is boxy: flat on top with steeper sides).

3. The trapezoidal mode with the same period of float, but run in such a way (by increasing the rating) as to require the same total rower power as in the first example.

The results are tabulated as follows:

  Mode:                         1 (Triangular)   2 (Trap.)       3 (Trap.)
  ===========================================================================
                                 Acc.  Dec.
  Periods (% of mass excursion)  40-20-40         25-50-25        25-50-25
  Rating, 1/min                  30.00            30.00           31.29
  Average shell speed, m/s        4.331            4.336           4.383
  Time for 2000m, s             461.8            461.2           456.3
  Total rower power, W          513.8            481.3           513.3 (equal)
  System mechanical eff.          0.56             0.62            0.60
  Footboard force, N (max.)     729 (front stop) 787             934
  Work in recovery phase, J     171              107             127

Increasing "float" from 20% to 50% in the return motions of the torso and the slide has permitted an average speed increase (Mode 3.) of about one percent; small, but enough to save about six seconds in 2,000 meters. The work done in the recovery phase has decreased 26%; the overall efficiency has increased 7%.

Note that, by itself (Mode 2.), switching from the triangular to the trapezoidal mode- at the same rating- has no effect on the average shell speed.

Achieving float seems not easy, as it requires increased body forces- 28% in this example- to boost the accelerations required at either end of the excursion period. Is the peak leg force required- 934N in this particular example- within a 90kg rower's physical capability? Seeking greater float than this has even higher force penalties. The increased body accelerations required produce steep discontinuities (Fig. 4-1 above) in the shell speed curve (including "check" at front stops); discontinuities which, heretofore, the conventional wisdom seems largely to condemn.

It seems to me unexplained as to how coaches take advantage of managing body motion in the free return. What is it that they urge their rowers to do? How effective is the result- as the possible gains seem small? How does a rower achieve or recognize float? Once a rower has achieved it how does he then know that he must correspondingly increase his rating in order to consolidate the advantage thus gained?

Reader comment on this topic is welcome:
E-mail: Atkinsopht